Understanding Order of Operations in Mathematics
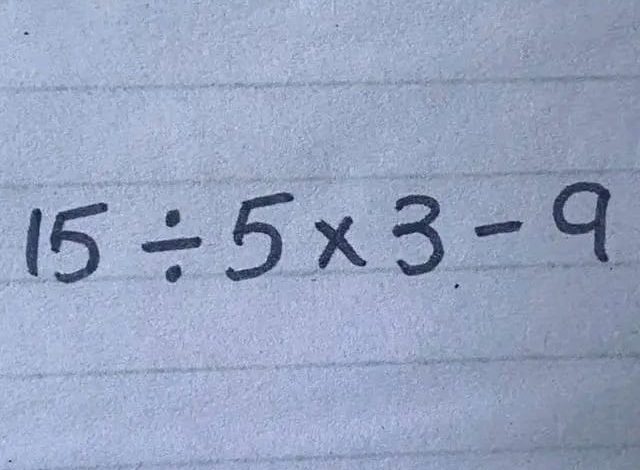
ADVERTISEMENT
Understanding Order of Operations in Mathematics
Introduction
Mathematics is a structured field of study, based on a set of rules that dictate the order in which operations should be performed to accurately solve expressions. One fundamental concept is the order of operations, crucial for ensuring consistent results. The equation “15 ÷ 5 × 3 – 9” provides a practical example to explore this concept.
Body The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right)), is essential for solving mathematical problems correctly. In the absence of parentheses and exponents, as in our example, we proceed with multiplication and division first.
For the given expression:
- Division First: 15÷5=315 \div 5 = 3
- Multiplication Next: 3×3=93 \times 3 = 9
- Subtraction Last: 9−9=09 – 9 = 0
Thus, following the correct order, the result of the expression “15 ÷ 5 × 3 – 9” is 0. Ignoring these rules can lead to significantly different and incorrect results, highlighting the importance of this systematic approach in mathematics.
ADVERTISEMENT
Conclusion The order of operations is more than just a mathematical formality; it is a critical framework that ensures the integrity and reliability of problem solving in mathematics. By working through the expression “15 ÷ 5 × 3 – 9”, we see how each step impacts the overall solution, reinforcing the necessity of applying these operations in their correct sequence. This not only helps in achieving the correct answer but also in understanding the logical structure of mathematical expressions.




