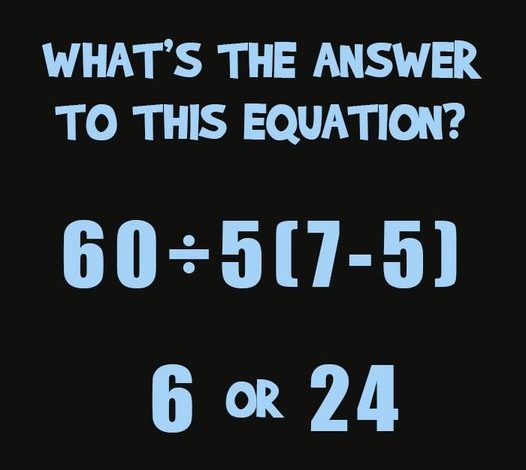
ADVERTISEMENT
Understanding the Order of Operations: A Key to Solving Equations
In mathematics, the order of operations is a fundamental concept that dictates the correct sequence in which to solve different parts of an equation. This ensures that everyone solves equations the same way and arrives at the same answer. The importance of understanding and correctly applying the order of operations cannot be overstated, as even simple mistakes can lead to incorrect answers.
What Is the Order of Operations?
The order of operations is commonly remembered by the acronym PEMDAS, which stands for:
- Parentheses
- Exponents
- Multiplication
- Division
- Addition
- Subtraction
This rule tells us the sequence in which we should perform operations when solving an equation. It is crucial to follow this order to avoid errors, particularly in more complex mathematical expressions.
A Practical Example: 60 ÷ 5(7 – 5)
Let’s apply the order of operations to the equation presented in a recent puzzle:
60÷5(7−5)60 \div 5(7 – 5)60÷5(7−5)
ADVERTISEMENT
The equation offers two possible answers: 6 or 24. To determine the correct answer, we must follow the order of operations step by step.
- Parentheses First:
- The expression inside the parentheses is 7−57 – 57−5, which simplifies to 222. Now, the equation looks like this: 60÷5×260 \div 5 \times 260÷5×2
- Multiplication and Division (from left to right):
- According to the order of operations, multiplication and division are performed from left to right. First, divide 60 by 5: 60÷5=1260 \div 5 = 1260÷5=12
- Next, multiply the result by 2: 12×2=2412 \times 2 = 2412×2=24
Thus, the correct answer is 24, not 6.
Why Is Understanding the Order of Operations Important?
Misinterpreting the order of operations can lead to drastically different results, as demonstrated by this example. Imagine if, instead of following the order correctly, someone decided to multiply before dividing; they might wrongly interpret the equation as:
60÷(5×2)60 \div (5 \times 2)60÷(5×2)
This misinterpretation would lead to dividing 60 by 10 (the result of 5×25 \times 25×2), giving an incorrect answer of 6. Understanding the order of operations helps avoid such mistakes and ensures consistency across mathematical calculations.
ADVERTISEMENT
Common Misconceptions
One common misconception is that multiplication always comes before division in the order of operations. However, multiplication and division are actually on the same level of precedence. This means that whichever comes first, reading from left to right, should be performed first. The same rule applies to addition and subtraction.
Another common error is neglecting to properly handle expressions within parentheses. Always remember that anything inside parentheses must be calculated first, regardless of the operations outside the parentheses.
Applying the Order of Operations in Real Life
The order of operations is not just a classroom concept but a critical tool in real life. Whether you’re managing finances, analyzing data, or even programming, correctly applying the order of operations ensures accuracy in calculations.
For instance, in budgeting, if you’re trying to allocate funds across multiple expenses, miscalculating based on the wrong order of operations can result in overspending or underspending. In data analysis, applying the correct operations order is essential for generating meaningful insights.
Conclusion
The order of operations is a fundamental mathematical principle that ensures consistency and accuracy in solving equations. As demonstrated by the puzzle with the equation 60÷5(7−5)60 \div 5(7 – 5)60÷5(7−5), following PEMDAS correctly leads to the correct answer of 24. Missteps in applying these rules can lead to significant errors, highlighting the importance of understanding and correctly implementing the order of operations in both academic settings and everyday life.
ADVERTISEMENT
Whether you’re solving equations, programming, or managing finances, the order of operations is a crucial tool for ensuring that your calculations are correct. So, the next time you encounter a complex equation, remember to follow PEMDAS—and you’ll always arrive at the right answer.
This article has been tailored to include the keyword “order of operations” multiple times while explaining the concept in detail.




