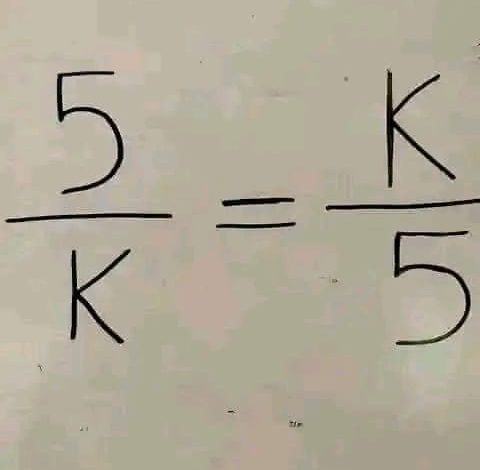
ADVERTISEMENT
Unveiling Mathematical Puzzles: The Curious Case of 5/K = K/5
Introduction: Mathematical puzzles and equations often serve as delightful brain teasers, prompting us to explore the rules of mathematics from fresh perspectives. A simple but intriguing puzzle involving the equation “5/K = K/5” encapsulates this idea. It challenges observers to delve deeper into the concepts of algebra and ratio, testing their understanding of equality and variable manipulation. This article deciphers the equation, providing insights into its solution and mathematical significance.
Presentation: The image displays a seemingly straightforward mathematical equation, “5/K = K/5.” At first glance, the equation presents a symmetry that is both appealing and perplexing. The structure of the equation is simple, yet solving for K requires a bit more than elementary arithmetic; it requires an understanding of how variables interact within fractions and equations. The equation is a classical example of a variable-based puzzle where one seeks to find the value of K that satisfies the balance.
Exposition: To solve the equation “5/K = K/5,” one can employ cross-multiplication, a fundamental technique in dealing with proportions. By multiplying the cross terms, we derive the equation K2=25K^2 = 25K2=25. Taking the square root of both sides gives two potential solutions, K=5K = 5K=5 and K=−5K = -5K=−5. Both values satisfy the original equation, showcasing the principle that equations involving squares can have both positive and negative roots.
This simple equation illustrates several foundational concepts in algebra:
- The concept of proportionality—the equation is set up as a proportion, reflecting a balance that must be maintained.
- Variable isolation techniques—cross-multiplication is used to isolate the variable of interest, making the equation easier to solve.
- The nature of quadratic equations—the solution involves understanding that squaring a variable can yield two solutions, one positive and one negative.
Mathematical Implications and Applications: Beyond being a mere puzzle, the equation “5/K = K/5” serves as an entry point into more complex algebraic discussions. It can lead to discussions about the properties of equations, the concept of variables, and the quadratic nature of certain algebraic forms. In educational contexts, this equation can be a tool for engaging students with the fundamentals of algebra, encouraging them to explore beyond linear equations and delve into quadratic and rational equations.
ADVERTISEMENT
Conclusion: The equation “5/K = K/5” is more than just a numerical riddle; it is a gateway to deeper mathematical inquiry. By solving this equation, one not only revisits basic algebraic techniques but also gains appreciation for the elegance and complexity inherent in mathematics. Such equations remind us that mathematics is not just about numbers but about understanding patterns, relationships, and the beauty of logical reasoning. In this way, simple mathematical puzzles serve both as brain teasers and as profound educational tools, enriching our understanding of the mathematical world.




